JJY受信機の設計（理論編）

2025/11/16

全体構成

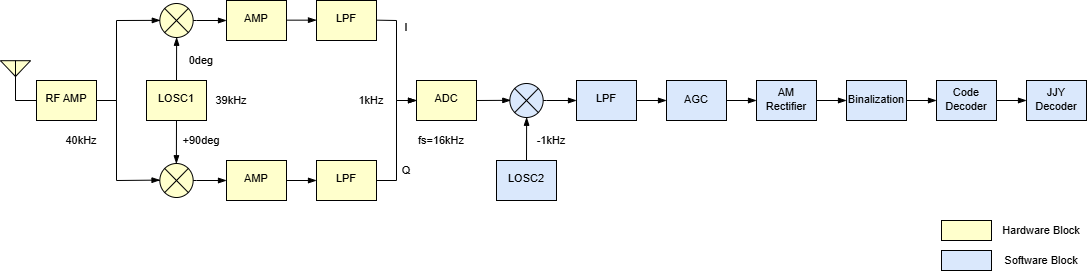
図1 全体ブロック図

今回設計したSDRのJJY受信機の全体ブロックは上記の通りです。40kHzからRF信号を直交ミキサーで1kHzのI,Q信号を生成し、ADCでサンプリングし、ソフトウェアで復号する受信機です。I,Q信号の周波数を0Hzにする方法も考えられますが、JJYの信号は矩形波なので、ADCへの入力のAC結合を通過できない可能性を考慮して、1kHzとしています。（DC結合にするとAMPの出力段でI、Q信号のコモン電圧を合わせる必要が出てきます）

RF信号からI,Q信号の生成

ミキサー段では、RF信号に位相が90degずれたLOSC（局部発振）の波形を混合し、90degずれた2つの信号を生成します。\( \omega_0 \)をRF信号の角周波数、\( \omega_1 \)をLOSC1の角周波数とすると、混合後の信号は下記のようになります。cos波はsin波より位相が90deg進んでいるので、図1の上段が下記の式(1)に、下段が式(2)に相当します。式(1)、(2)ともに\( (\omega_0 + \omega_1) \)の角周波数の成分と\( (\omega_0 - \omega_1) \)の角周波数の成分の和に変換されます（第1項+π/2は時間に依存しないので無視します）。後段のアンプ介し、LPF(Low Pass Filter)で\( (\omega_0 + \omega_1) \)の周波数成分を除去することで、\( (\omega_0 - \omega_1) \)の周波数のI(in-phase),Q(Quadrature)信号が生成できます。I信号は、Q信号に対して90deg位相が進んでいるので、式(1)よりI信号、式(2)よりQ信号が生成されます。以降、I信号はcos波、Q信号はsin波と考えると分かりやすいかと思います。

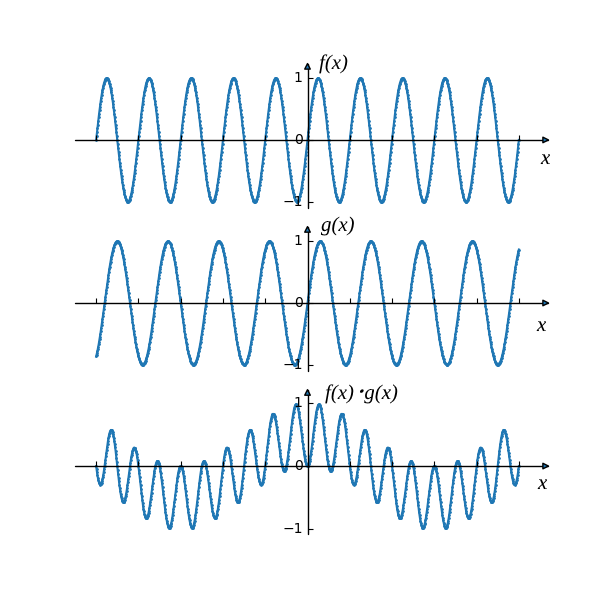
\[ \begin{align} \sin{{\omega}_0t}\sin{{\omega}_1t} &= -\frac{1}{2}(\cos{({\omega}_0t+{\omega}_1t)}-\cos{({\omega}_0t-{\omega}_1t)})\\ &= \frac{1}{2}(\sin{({\omega}_0t+{\omega}_1t-\frac{\pi}{2})}+\cos{({\omega}_0t-{\omega}_1t)}) \tag{1} \end{align} \] \[ \begin{align} \sin{{\omega}_0t}\cos{{\omega}_1t} &= \frac{1}{2}(\sin{({\omega}_0t+{\omega}_1t)}+\sin{({\omega}_0t-{\omega}_1t)})\\ &= \frac{1}{2}(\cos{({\omega}_0t+{\omega}_1t-\frac{\pi}{2})}+\sin{({\omega}_0t-{\omega}_1t)}) \tag{2} \end{align} \]

周波数の異なる信号の混合（掛け算）のイメージは下記のようになります。混合された波形には、２つの周波数の波形が見えるかと思います。

矩形波のフーリエ級数展開

上記のミキサーではRF信号とLOSC1信号の積をとることを想定していますが、実際の回路は下記のようにアナログスイッチで、RF信号をLOSC1の方形波でスイッチングする回路を用います。

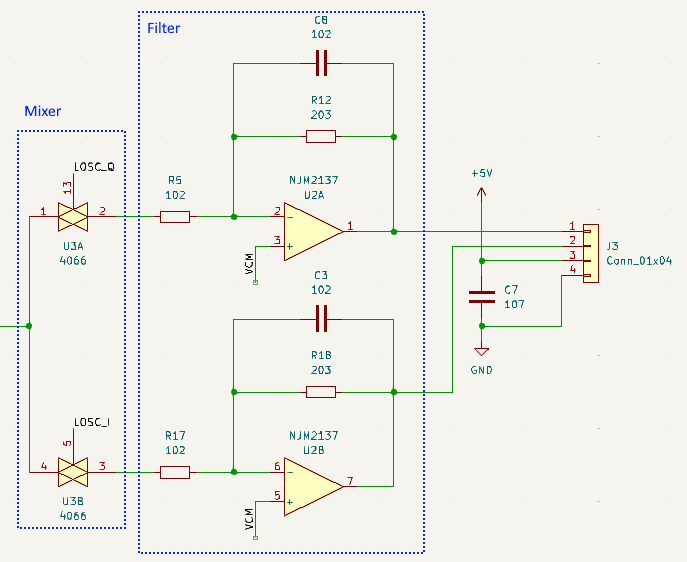
I,Qの片側だけの信号だけで考察します。RF信号をLOSC1信号でスイッチングすると、アナログスイッチONのとき（LOSC1信号Hのとき）は、アナログスイッチの出力はRF信号がそのものになります。アナログスイッチOFFの時は、アナログスイッチの出力は反転増幅回路で受けているので、common電圧（片電源では通常1/2VCC）に固定されます。RF信号、LOSC1信号、アナログスイッチの出力信号を下記の\(r(x)\)、\(l(x)\)、\(m(x)\)と想定すると、\(m(x)=r(x)l(x)\)となり、ミキサーとなっていると考えられます。

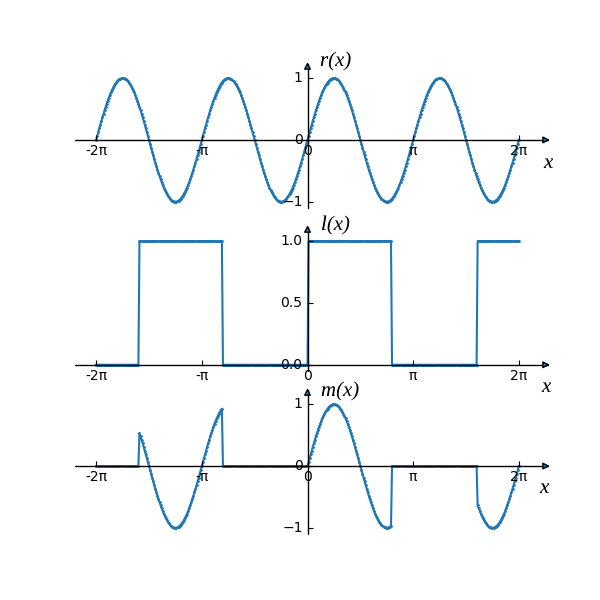
ただし、\(l(x)\)は三角関数ではありませんので、式(1)、(2)をそのまま適用できません。\(l(x)\)のフーリエ級数展開を考えます。関数\(f(x)\)のフーリエ級数展開は下記の式となります。\(f(x)\)は連続関数であり、周期関数である必要があります。

\[ \begin{align} f(x) &= \frac{a_0}{2} + \sum^\infty_{n=0}\{a_n\cos(nx)+b_n\sin(nx)\} \tag{3}\\ a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx\space(n=0,1,2,...)\\ b_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx\space(n=1,2,...) \end{align} \]

\(l(x)\)をここでは\(f(x)\)として、下記のように定義します。

\[ \begin{align} \begin{cases} 0 & ({-\pi} \geq x < 0) \\ 1 & (0 \geq x < {-\pi}) \end{cases} \end{align} \]

\(a_0\)を計算すると下記のようになります。

\[ \begin{align} a_0 &= \frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)dx} \\ &= \frac{1}{\pi}\int_{-\pi}^{0} 0 \cdot dx + \frac{1}{\pi}\int_{0}^{\pi}1 \cdot dx \\ &= 1 \tag{4} \end{align} \]

\(a_n\)を計算すると下記のようになります。

\[ \begin{align} a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\cos(nx)dx} \\ &= \frac{1}{\pi}\int_{-\pi}^{0} 0 \cdot \cos(nx)dx + \frac{1}{\pi}\int_{0}^{\pi}1 \cdot \cos(nx)dx \\ &= 0 \end{align} \]

\(b_n\)>を計算すると下記のようになります。

\[ \begin{align} b_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\sin(nx)dx} \\ &= \frac{1}{\pi}\int_{-\pi}^{0} 0 \cdot \sin(nx)dx + \frac{1}{\pi}\int_{0}^{\pi}1 \cdot \sin(nx)dx \\ &= \frac{1}{\pi}\left[ -\frac{1}{n}\cos(nx) \right] ^{\pi}_{0} = -\frac{1}{n\pi}\left( \cos(n\pi)-1 \right) \\ &= \begin{cases} 0 & n=2m \space (m=1,2,...) \\ \dfrac{2}{n\pi} & n=2m-1 \space (m=1,2,...) \tag{5} \end{cases} \end{align} \]

式(4)、(5)を式(3)に代入すると展開式が得られ、DC成分とf(x)の周期の奇数倍（1, 3, 5, ...）の周波数が含まれることが分かります。（今回、f(x)が奇関数になるように位相を設定してたので、b_n項しか残っていませんが、位相をずらせばa_n項も出てくることは想像できるかと思います。ただし、含まれる周波数成分は変わりません。）これで、DC成分や3倍以上の周波数の高調波成分はLPFにより除去されますので、上記のミキサーの処理が可能がことがわかると思います。

今回は搬送波40kHzのJJY信号に、39kHzの局部発振の信号を混合し、1kHzの信号に変換します。もともと4kHzで設計していたこともあり、LPFのカットオフは7.9kHzとしています。LPFのカットオフはI,Qの信号のレベルに影響しないように、カットオフを出力信号の2倍程度に設定しました。

複素信号とは

\[ A(\cos\theta + j \sin\theta)=Ae^{j\theta} \]

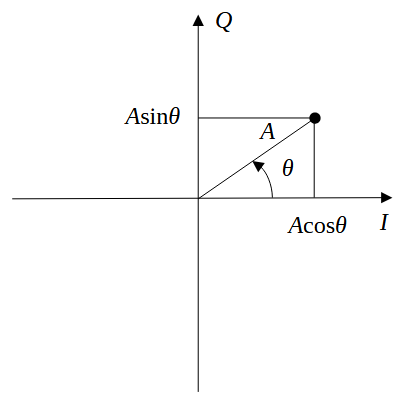
I, Q信号の値をI,Qの平面に描画し、これを複素平面とみなせば、振幅と位相を同時に表すことができる量となっていることが分かります。複素数としては絶対値と偏角に相当します。この表現を使うことで、周波数変換や変復調が複素計算で行うことができるようになります。
AM変調波の場合は、振幅を時間変化する量として、位相は一定の角周波数で時間変化するものとなるので、下記のように表現できます。

\[ f(t)=A(t)(\cos\omega_c t + j \sin\omega_c t)=A(t)e^{j\omega_c t} \]

I,Qの平面上では、原点を中心としてして原点からの距離を変えながら回転する点となります。回転の角周波数がω_c、原点からの距離がA(t)となります。I、Q信号の値はこの点のI軸、Q軸の値であり、時間波形はI軸への写像、Q軸への写像となります。注意すべき点としては、ω_cが正であれば左回転、負であれば右回転になり、負の周波数が表現できます。

ADCによるサンプリング

サンプリング定理からは信号の周波数の2倍以上の周波数でサンプリングすれば原信号を再現できるはずですが、信号解析を行うアプリケーションではより高い周波数でのサンプリングが必要です。下記は、信号周期の2倍の周波数でサンプリングする場合（上）と10倍の周波数でサンプリングする場合（下）のイメージです。

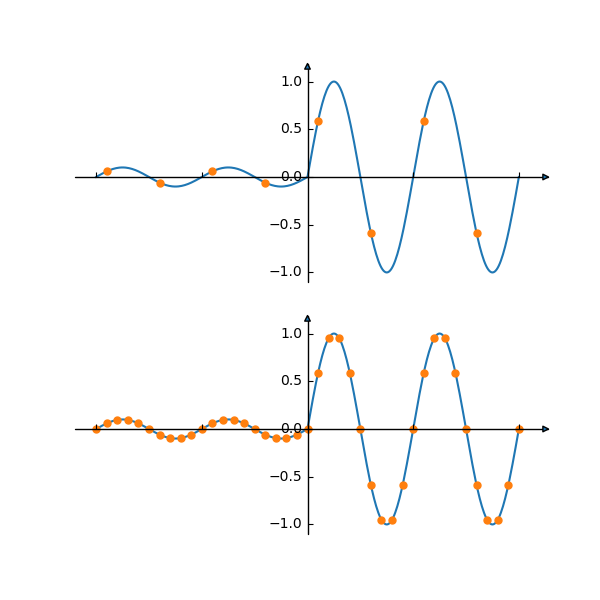
今回は1kHzのI,Q信号を16kHzでサンプリングします。
また、ADCする信号はアンチエイリアスフィルタ(antialias filter)で、ナイキスト周波数（サンプリング周波数の1/2）以上の周波数成分を除去する必要があります。これはサンプリング定理より、ナイキスト周波数より高い周波数成分は、サンプリングすることでナイキスト周波数内に折り返して重畳されてしまうからです。ミキサーの後段のLPFのカットオフ周波数を7.9kHzとしていますので、これがアンチエイリアスフィルタを兼ねていると考えることができます。ちなみに、カットオフ周波数でのゲインは-3dB(\( 1/\sqrt{2} \))ですので、フィルタ構成部品の誤差によるI,Qでの振幅の誤差を少なくするためには、信号の周波数よりカットオフ周波数は大きく（１次のフィルタであれば2倍程度）設定することが望ましいと考えられます。さらに、今回はオーディオ用のADC(ΔΣ型)を用いますので、ADC内にもアンチエイリアスフィルタが搭載されています。
今回ディジタル処理には16bitマイコンを用いますので、ADCでの量子化ビット数は16bitとしています。

複素演算による周波数変換

AD変換した信号をベースバンドの周波数まで落とします。後段でBPFでなく、LPFで信号選択ができるよになります。
複素数の掛け算は偏角の足し算になりますので、複素信号の周波数変換は２つの複素信号の掛け算で行うことができます。周波数を上げたい場合は正の周波数の信号を、周波数を下げたい場合は負の周波数の信号を掛け算します。具体的には、２つの信号のサンプル値をそれぞれ掛け算します。指数表現と、要素での表現の掛け算は下記になります。

\[ e^{j2{\pi}f_s}e^{j2{\pi}f_l}=e^{j2{\pi}(f_s+f_l)} \] \[ (i_s+jq_s)(i_l+jq_l)=(i_si_l-q_sq_l)+j(i_sq_l+q_si_l) \]

掛け合わせる局部発振信号は発信周波数をf_l、サンプリング周波数をf_sとすると下記になります。、

\[ i[n]=\cos{2\pi\frac{f_l}{f_s}n} \] \[ q[n]=\sin{2\pi\frac{f_l}{f_s}n} \]

式から分かるように、サンプル値をテーブルで用意するためには、つまり1周期ごとのサンプル値を同じ値にするためには、\( f_l \)を\( f_s \)の約数にする必要があります。

LPFによる周波数選択

FIRフィルタで周波数選択を行います。通過帯域幅とタップ数はPCの検証環境などで決めます。フィルタ係数の生成方法は別ページで説明させて頂きます。タップ数が多いとフィルタの周波数分解能が上がりますが、計算時間がかかります。また、通過帯域を狭めると選択度は上がりますが、矩形波の波形がなまります。これらのトレードオフを考え設定します。
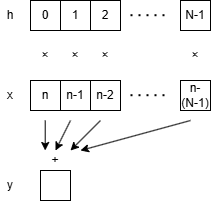
時間領域でのフィルタ処理は畳み込み演算になります。サンプル時間nの時の入力値をx[n]、出力値y[n]、フィルタ係数をhとすると下記のようになります。

\[ y[n]=\sum^{N-1}_{k=0}{h[k]x[n-k]} \]

これから、タップ数Nとした場合、N-1の過去の入力値を保持する必要があります。x, hのバッファと演算のイメージは下記のようになります。 x, hのバッファの先頭から最後までx, hを乗算し、積算していきます。MAC演算(Multiply and Accumulate opertion)と呼びます。ただし、FIRのフィルタ係数は奇数個で遇対象なので、実際にはフィルタ係数hはN/2+1を保持し、0番目→N/2番目→0番目と折り返して読み込み使用します。また、今回固定小数点で計算しますので、フィルタ係数は有効桁数ぎりぎりまで2の累乗倍しておきます。2の累乗倍であるのは、フィルタ演算後、シフト演算で桁調整するためです。

AGC

フィルタリングを行うと余分な周波数成分が省かれてレベルが減少しますので、この段階でAGC(Auto Gain Control)の処理を行います。AGCはラジオの場合出力音声のレベルを一定に保つために行いますが、JJYの受信においても0, 1の判定をするための閾値をなるべく一定に保つために行います。今回固定小数点で処理していますので、有効桁数を稼ぐ意味もあります。
アナログのラジオ受信回路のAGCは、検波後の信号にLPFをかけて、初期の増幅段に帰還します。ディジタル処理では、フィルタ後の信号の振幅の最大値を一定期間で計算し、目標の振幅レベルへの倍率（ゲイン）を計算し、信号値に掛け算します。

下記がSdrStudyのAGCコードになります。maxLevelは1024サンプルの最大値です。つまり、1024サンプルの最大値を0.1になるように現在の信号をスケールします。

gain = 1.0;   // デフォルトのゲイン値を設定
if (maxLevel != 0.0)			// 0による除算を避ける為の処理
{
    gain = 0.1 / maxLevel;	// 最大振幅が0.1になるようなゲインを算出
    if (gain > maxgain)	    // ゲインが最大値より大きいか？ 
        gain = maxgain;		// ゲインを最大値に制限
}
if (gain < gainavarage / agctime)	// 強い信号レベルの場合には
    gainavarage = gain * agctime; 	// すぐにAGCレベルを反映させる
else
{       // 弱い信号レベルなら
    gainavarage = gainavarage - gainavarage / agctime + gain;	// ゆっくりゲインを上昇させる
    gain = gainavarage / agctime;   // AGCに時定数を持たせる
}

強い信号レベルの場合には即時反映ですが、弱い信号レベルならゆっくりゲインを上昇させる処理が入っています。ゆっくりゲインを上昇させる処理はIIRフィルタになります。IIRフィルタの処理前のgainを\( g_0 \)、フィルタ処理後のgainを\( g \)、agctimeを\( Tg \)とすると下記のフィルタの式と同様になります。\( gT \)がgainaverageに当たります（変数名はやや分かりずいと思います）。サンプリング周期×Tで、サンプルの最大値から計算されたゲインが反映されると考えられます。

\[ g[n] = \frac{{(T-1)g[n-1]+g_0[n]}}{T} \]

ただし、今回は数値はQ1.15の固定小数点でdsPICに実装しますので、上記の計算を下記のように修正します。

if (++sampleCount >= sampleMaxCount)
{
    if (max > 0)
    {
        short gain = (short)(targetAmp / max);
        accGain = accGain - (accGain >> applyTimeBits) + gain;
        gain = (short)(accGain >> applyTimeBits);

        gainShift = 16 - FindFirstOneFromLeft(gain);
        gainFrac = (short)(gain - (1 << gainShift));
    }
    sampleCount = 0;
    max = 0;
}

まず、1サンプルごとに処理を行うので、検波後のサンプル値（複素信号の絶対値）の最大値はsampleMaxCountサンプルで検出します。JJY信号の0,1のパルスに被る時間としなくてはなりません。その後、ターゲットの振幅targetAmpを検出した最大値maxで割り、必要な倍率gainを計算します。gainは整数値のみで表現します。整数部と小数部の両方に有効桁がある演算を固定少数点演算で行うのはかなり難しいためです。フィルタの時定数は2の累乗とし、何乗かをapplyTimeBitsとします。こうすることで、時定数での除算をシフト演算で行うことができます。最後に、フィルタしたgainを2の累乗と残りの倍率に分けます。dsPICにはFindFirstOneFromLeftという命令があり、MSBから数えて1が出現するビット数を返してくれますので、これから2の累乗部分をとりだしgainShiftとし、残りの倍率をgainFracとします。フィルタはdsPICの40bitのアキュムレータで計算されますが、アキュムレータから値を取り出すと、16bit値になってしまうため、AGCの処理はこのアキュムレータから取り出すときに、gainShift分シフトして取り出した値と、gainShift分シフトせずに取り出した値のgainFrac倍の値を加算することで行います。

AM検波

AM検波は複素信号の振幅（絶対値）を計算するだけです。ただし、そのまま計算すると、平方根を計算する必要が出てきますので、CORDIC(COordinate Rotation DIgital Computer)を用いて距離を計算します。CORDICはその名の通りで、XY平面で第1象限中の任意の点の原点からの距離と角度を、加減算とシフト演算で計算する方法です。

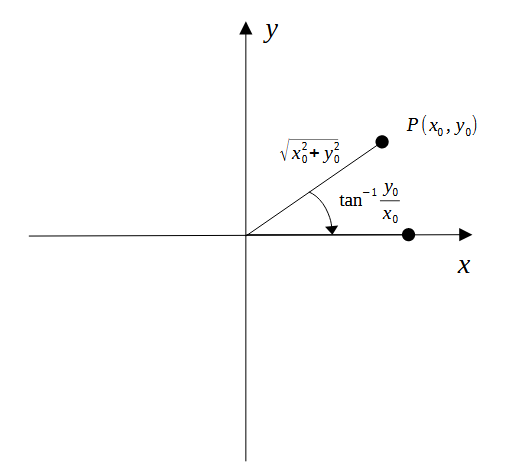
原理は上記のように、任意の点Pを回転しx軸にもっていくことで、距離はx軸を値で、角度は回転した角度で取得することができます。CORDICの更新式は下記になります。複数回の回転を行い、x軸に点Pを回転します。

\[ \begin{pmatrix} x_n \\ y_n \end{pmatrix} = \begin{pmatrix} 1 & p\delta \\ -p\delta & 1 \end{pmatrix} \begin{pmatrix} x_{n-1} \\ y_{n-1} \end{pmatrix} = \] \[ \delta=2^{-(n-1)}=1,\frac{1}{2},\frac{1}{4},\frac{1}{8},... \] \[ p=1\space\text{or}\space{-1} \tag{6} \]

これがなぜ回転の式になるかは、\( p=-1, \delta=\tan{\theta} \)と置いて、下記のように変形すると分かります。

\[ \begin{pmatrix} 1 & -\delta \\ \delta & 1 \end{pmatrix} = \frac{1}{\cos{\theta}} \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} = \sqrt{1+\tan^2{\theta}} \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} = \] \[ \sqrt{1+\delta^2} \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} = \sqrt{1+\delta^2} R(\theta) \]

これから、\( \sqrt{\delta^2+1} \)倍の項がつきますが、平面の回転行列\( R(\theta) \)になっていることが分かります。
式6に戻ると、σは2の累乗分の1となっており、\(x_{n-1}, y_{n-1}\)に対して、\(x_n, y_n\)は右シフトと加減算で計算できることが分かります。N回目の回転角は\(\theta=\tan^{-1}\sigma=2^{-(n-1)}\)となり、予め計算しておくことができます。また、計算回数も予め決めますので、\( r_n=\sqrt{\delta^2+1} \)とおくと、\( r_n \)も予め計算可能です。N=15までを計算すると下記のようになります。

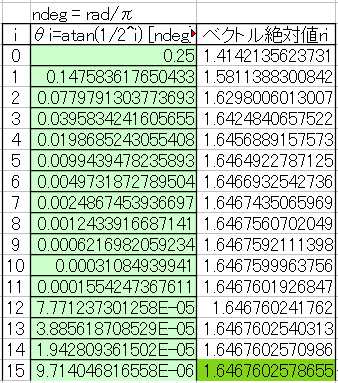
\(\theta_0\)は\(\tan^{-1}\dfrac{1}{2}=45^\circ \)になりますので、計算できるのは第1象限の角0°～90°までになりますので、それ以外の象限角はx,y軸対象で第1象限へ変換し計算します。実際の計算は下記のように、\(\theta_0\)からステップごとに現在の角度が0より大きければ、次のステップの角を引き、0より小さければ次のステップの角を足し、0に近づけています。ステップ数は計算結果の精度に反映されますが、1ステップごとに右シフト量が増えていくため、有効ビット数と同じにすべきであることが分かります。今回はdsPIC33FでQ1.15で実装しますので、16ステップで計算します。精度を上げるために、計算中のビット数はそれより多くする必要があります。

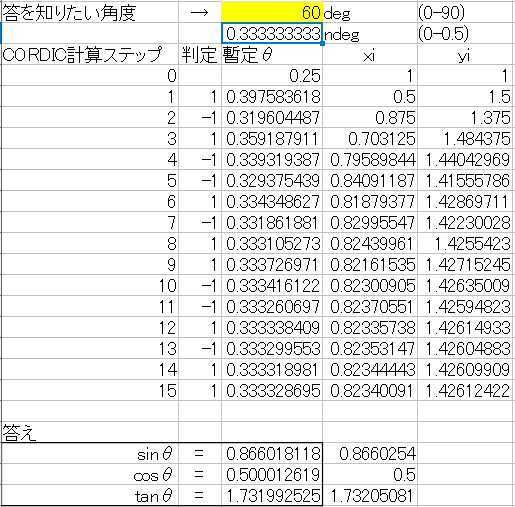
2値化

AMの振幅を0,1の2値化します。JJYのパルスのHighは振幅100%、Lowは振幅10%ですが、100%は振幅の最大値です。AGCが正しく効いていれば理論的には、固定値の閾値での2値化が可能ですが、固定小数点でのAGCの精度はあまりよくないため、最大振幅、最小振幅の中間値を閾値として2値化します。閾値は下記の手順で計算します。

一定時間で平均値(ave)を計算します。これでパルスノイズの影響を削減します。
平均値の一定時間での最大値(norm_inst_max)、最小値(norm_inst_min)を検出し、中間値(temp_center)を計算します。（パルスのHigh, Lowの時間に等しくなりませんので、単純にaveの平均値を閾値とはできません）
中間値(temp_center)にACGと同じフィルタをかけ、最終的な閾値とします。（level_det_cent）
閾値を使用し、各サンプルの振幅を2値化します。

図では下記のイメージになります。

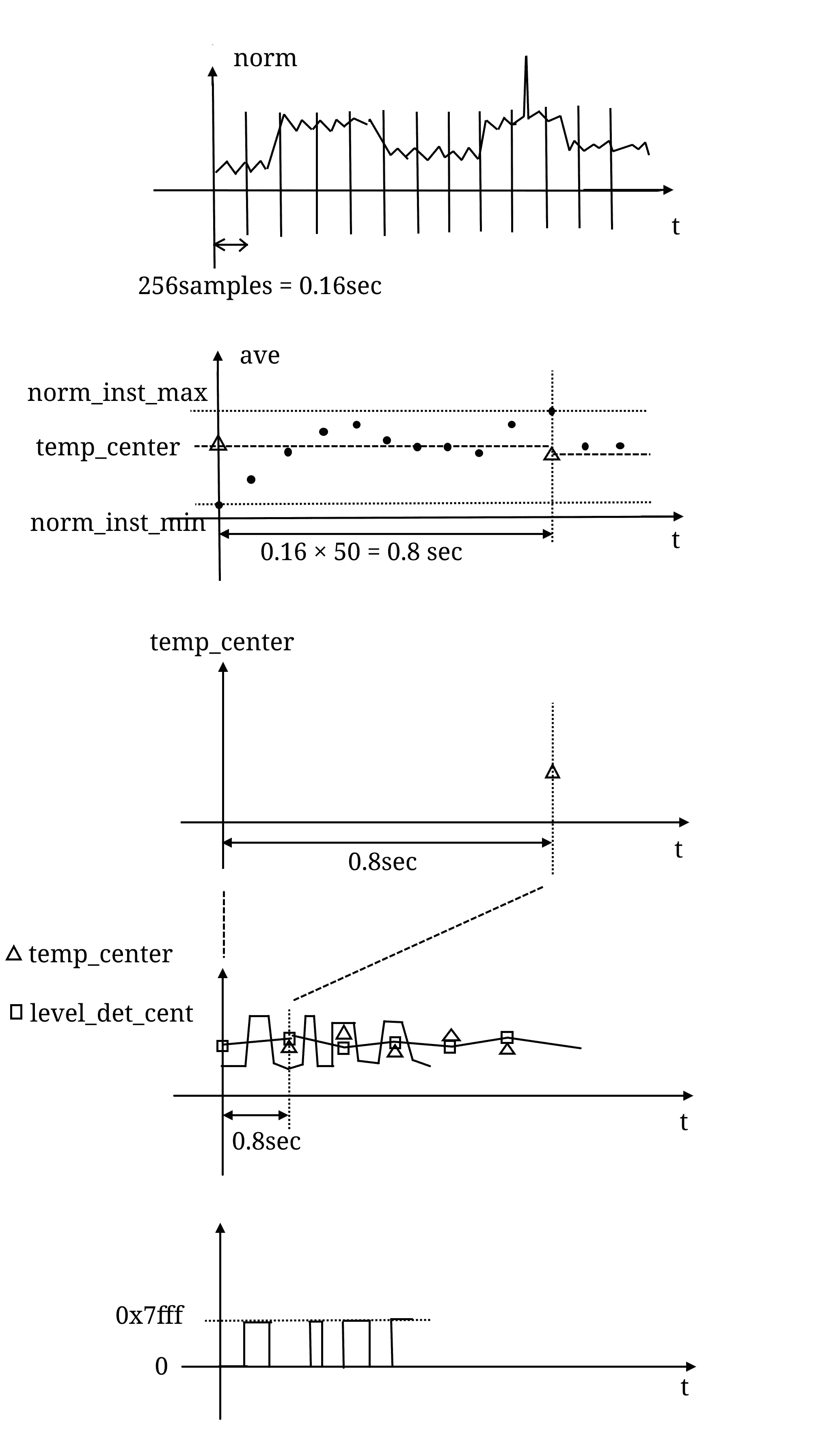
コードデコード

2値化された振幅から、JJYのコード（P, 0, 1, E）をデコードします。2値化された振幅のHigh区間、Low区間の時間を計測しデコードします.が、下図のようなノイズによる瞬間的なHigh, Lowの反転が起きますので、0, 1を確定する期間を定義して0, 1を決めます（デバウンス処理と同様）。確定期間だけ遅延が発生しますが、コードのデコードの成功率を上げることができます。このブロックの出力はP(Position Code)、0(0値)、1(1値)、E(Error)の4通りになります。

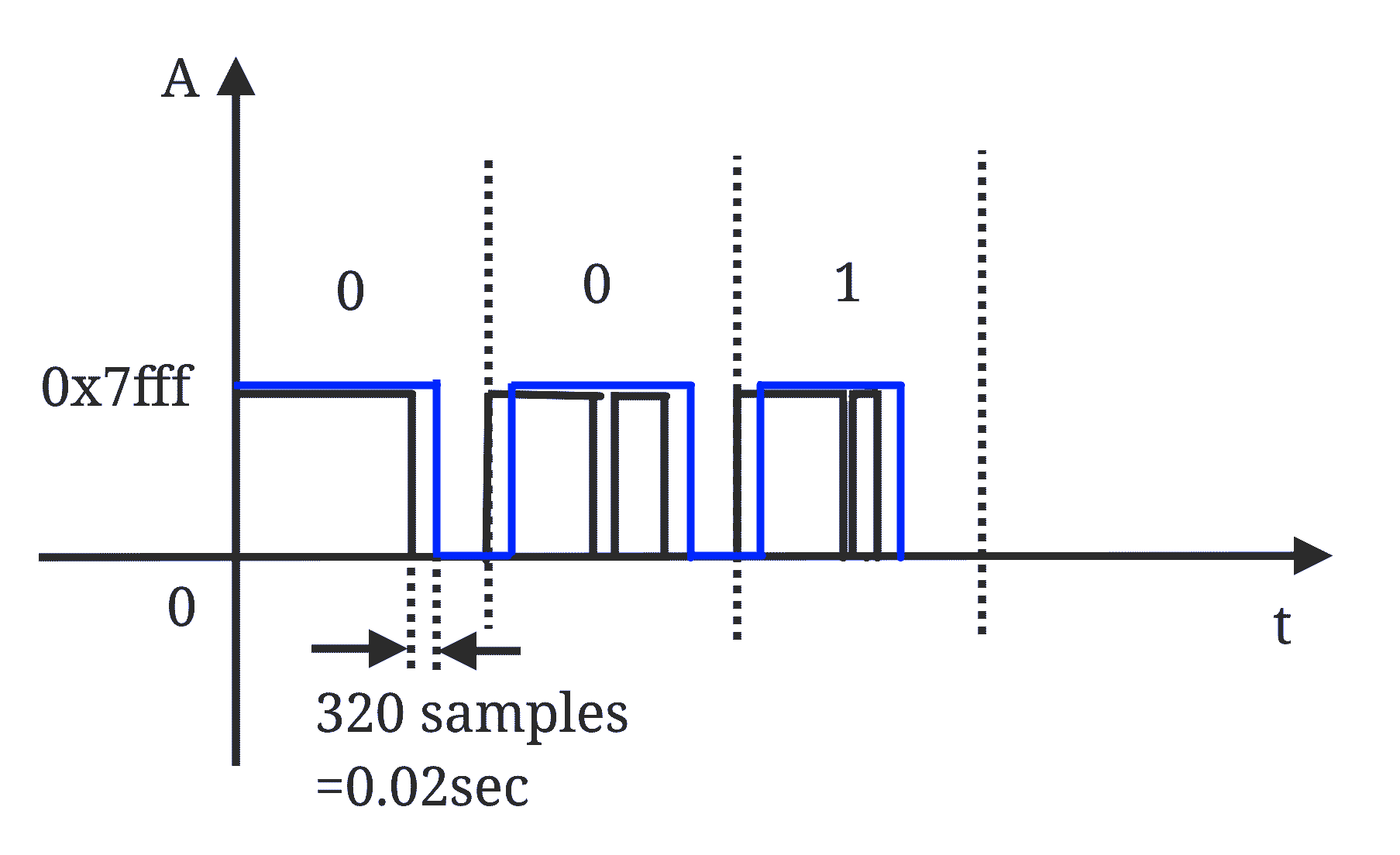
JJYデコード

コードデーコードブロックの出力のコードから、日付時刻をデコードします。単純に下図のステートマシーンで実装します。まず、ポジションコード2つのの連続で0秒のポジションマーカを判別します。Wait P0ステートは59秒、60秒のP0を待つ状態です。その後、10秒ごとのブロックを１つの状態として、分、日、年、曜日を取得していきます（状態の名前はブロックで主に受信している情報の名前としています）。毎時15分、45分は5番のブロックがJJYのモールス信号になるため、第4ブロックまで受信したときに、15分、45分であれば、P5を待つ状態に入ります。下記のステートマシーンでは、JJYコード中の0埋めになっている部分はDon't Careとしてあります。

dsPIC33FJ64GP802への実装の補足

dsPIC33FJ64GP802への実装では、上記のソフトウェアブロックはDCIの割り込みにて、1サンプル周期で実行します。DSP命令を効率よく使うため、コードデコードまではアセンブラで実装、JJYデコードのみCで実装しています。条件分岐の多いJJYデコードはアセンブラで実装するのが難しかったためになります（バグを作りやすい）。

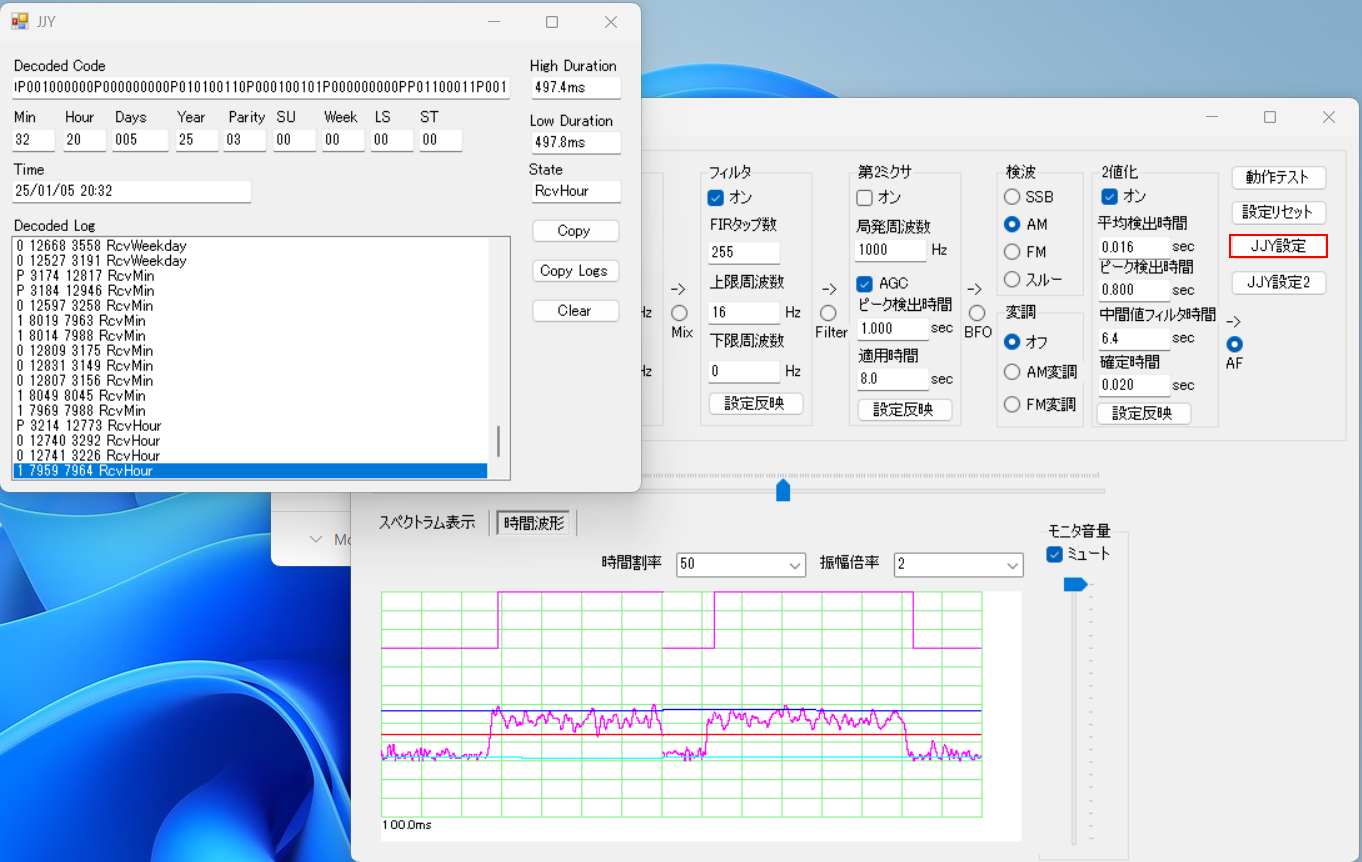
SdrStudy改

RF World No.22付属のSdrStudyに上記のJJYのデコード関連の機能と、時間波形表示機能を実装したバージョンを下記にアップロードしました。アーカイブを展開後、SdrStudy\bin\Release\SdrStudy.exeを実行し、[JJY設定]もしくは[JJY設定2]ボタンをクリックすると、JJYデコードの様子が確認できます。SdrStudyそのものの使い方はRF World No.22をご参照ください。ソースコードも付属していますので、各処理の具体的な実装も確認できるかと思います。

戻る